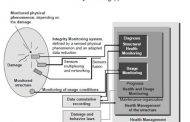
هندسه فراکتال و مفهوم آن در معماری

هندسه فراکتال و مفهوم آن در معماری

هندسه فراکتال : فراکتال از ریشه کلمه یونانی فراکتوس به معنی سنگ خرد شده است.

فراکتال به اشکالی شبیه به هم که از یک خانواده اند و خود متشابه هستند گفته می شود که بطور بی نظم در کنار یکدیگر قرار می گیرند.

این شکلها که نظم مشخصی ندارند از هارمونی و نظم در عین بی نظمی برخوردارند.

نمونه این هندسه در همه طبیعت در مقیاسهای مختلف دیده می شود. مانند کوهها، درختان، برگها و غیره

هندسهٔ فرکتالی وسیله و مفهومی نوین است که امکان توصیف ریختهای طبیعی را میسرکرده است.

اشکال هندسی طبیعی همچون کرات آسمان ودرخت کاج را به آسانی می‌توان با کره ومخروط توصیف کرد ولی بسیاری دیگر ازاشکال طبیعی به اندازه‌ای پیچیده هستند که حتی با ترکیبی از اشکال هندسه اقلیدسی قابل توصیف دقیق نیستند.

شکل گل‌کلم، ریخت کوهها، رویه یک فلز درمقیاس‌های میکروسکوپی نمونه‌هاییاز شکل‌های طبیعی هستند که توصیف آنها تنها توسط هندسهٔ فرکتالی ممکن است.

هندسه فراکتال

هندسه اقلیدسی – احجام کامل کره هات و هرم ها و مکعب ها و استوانه – بهترین راه نشان دادن عناصر طبیعی نیست ابرها و کوه ها و خط ساحلی و تنه درختان همه با احجام اقلیدسی در تضاد هستند و نه صاف بلکه ناهموار هستند و این بی نظمی را در مقیاس های کوچک نیز به ارمغان می آورند. که یکی از مهم ترین خصوصیات فراکتال ها همین است. این بدین معناست که هندسه فراکتال بر خلاف هندسه اقلیدسی روش بهتری برای توضیح و ایجاد پدیده هایی همانند طبیعت است. زبانی که این هندسه به وسیله آن بیان می شود الگوریتم نام دارد که با آن اشیاء مرکب می توانند به فرمل ها و قوانین ساده تری ترجمه و خلاصه شوند. فراکتال ها می توانند همه جا حتی در معماری نمود پیدا کنند.

فراکتال

هندسه طبیعت یا فرکتالها سالهاست که توسط معماران و ریاضیدانان متعددی مورد بحث و بررسی قرار گرفته و به کارگیری آن در معماری و هندسه مصنوع مورد شک و تردید، نقض یا دفاع واقع شده است. از یک سو معماران زیادی از جمله چارلز جنکس، پیتر آیزنمن، دنیل لیسکیند، فرانک گهری و … مدعی هستند که با برداشتی شخصی از این نوع هندسه و تقلید ظاهری آن به پارادیم جدیدی در طراحی معماری دست یافته اند و در سوی دیگر محققانی چون نیکوس سالینگاروس و کریستوفر الکساندر قرار دارند که با تسلط به دانش ریاضی فرکتالها تناسبات و معیارهای رفومی جدیدی برای نقد و طراح معماری ارائه داده اند.

هندسه فراکتال

اگر بخواهیم از دید کلی به بحث فرکتال نگاه کنیم آن را می توان به ۳ دسته تقسیم بندی کرد:

هندسه فرکتال: در این قسمت از دید ریاضی به فرکتال نگاه می شود که بیشتر مورد توجه ریاضی دان ها قرار گرقته اما پایه های قسمت های بعدی نیز می باشد، و تا با عناصر اصلی فرکتال و چگونگی ایجاد این فرم آشنا نشویم نمی توان فرم های مختلف و حجم های مختلف را شناسایی کرد.

فرم فرکتال: قسمت دوم این مقاله است، با توجه به اینکه، محصول هندسه فرکتال فرمی است که دقیقاً آن مشخصه های هندسی مربوطه را دارد. در این بخش فرم هایی همچون فرم های درخت، فرم های مندلبرت، فرمهای موجود در طبیعت، ایجاد فرم های رندوم (Random Fractal)، خود متشابهی (Self Similarity)، فرکتال در نقاشی (آثار نقاشانی چون جکسون پالاک) و … مورد بررسی قرار خواهد گرفت.

۲- فرکتال را در اثار چون جکسون پالاک و لاری پونز می بینیم.

فراکتال

حجم فرکتال (فرکتال در معماری): نتیجه فرم های مختلف می تواند به یک اثر معماری منتج شود لذا در این بخش حجحم های فرکتالی و آثار معماری مطرح می شود.

اما در هندسه:حجم فرکتال

هندسه فرکتالی پدیده ایست که چندی پیش پا به دنیای ریاضیات گذاشت.

واژه فرکتال در سال ۱۹۷۶ توسط ریاضیدان لهستانی به نام بنوئیت مندلبرات وارد دنیای ریاضیات شد.

او در سال ۱۹۸۷ پرفسوری خود را در رشته ریاضیات گرفت.

مندلبرات وقتی که بر روی تحقیقی پیرامون طول سواحل

انگلیس مطالعه می نمود به این نتیجه رسید که هر گاه با

مقیاس بزرگ این طول اندازه گرفته شود بیشتر از زمانی

است که مقیاس کوچکتر باشد.

از لحاظ واژه مندلبرات انتخاب اصطلاح فرکتال (Fractal) را

از واژه لاتین Fractus یا Fractum (به معنی شکسته)

گرفت تا بر ماهیت قطعه قطعه شونده که یکی از مشخصه های اصلی این فرم است، تاکید داشته باشد.

فرهنگستان زبان هم واژه بر خال را تصویب کرده و همچنین برای واژه فرکتالی واژه بر خالی را تصویب کرده است.

واژه فرکتال به معنای سنگی است که به شکل نامنظم شکسته شده باشد.

فرکتال از دید هندسی به شیئی گویند که دارای سه ویژگی زیر

باشد:

اول اینکه دارای خاصیت خود متشابهی باشد یا به تعبیر دیگر Self – similar باشد.

در مقیاس خرد بسیار پیچیده باشد.

بعد آن یک عدد بسیار پیچیده باشد.

بعد آن یک عدد صحیح نباشد (مثلاً ۵و۱)

برای درک بهتر نسبت به مشخصات بالا در فرم هندسی، بد نیست نمونه ای

که شاید تاکنون با آن برخورد کرده باشید مطرح شود:

خاصیت خود متشابهی فرکتالها

شیئی را دارای خاصیت خود متشابهی می گوییم: هر گاه قسمت هایی از آن با یک مقیاس معلوم، یک نمونه از کل شیئی باشد.

ساده ترین مثال برای یک شیئی خود متشابه در طبیعت گل کلم است که هر قطعه ی کوچک گل کلم متشابه قطعه بزرگی از آ« است.

همین طور درخت کاج یک شیئی خود متشابه است، چرا که هر یک از شاخه های آن خیلی شبیه یک درخت کاج است ولی در مقیاس بسیار کوچکتر.

همچنین در مورد برگ سرخس نیز چنین خاصیتی وجود دارد.

رشته کوهها، پشته های ابر،؛ مسیر رودخانه ها

و خطوط ساحلی نیز همگی مثال هایی از یک

ساختمان خود متشابه هستند.

هندسه فراکتال

عدم بعد صحیح

این بخش در فرکتال ها بسیار مهم است به طوری که خیلی از فرمها با این مشخصه از فرم هایی با هندسه اقلیدسی جدا می شوند.

محاسبه بعد فرکتال ها:

اگر بگوییم بعد خط، برابر یک باشد و نیز بعد صفحه، برابر دو باشد.

همچنین بعد فضا با عدد سه معرفی شود.

اما فرکتالها بر خلاف همه ی اینها بعد صحیح ندارند. بعد فرکتالها یک عدد کسری می باشد.

وقتی که گفته می شود بعد یک فرکتال ۲و۱ می باشد این بدین معنی است از خط پیچیده تر و اط صفحه ساده تر است.

محاسبه این بعد از یک سری فرمول های لگاریتمی بدست می آید که بررسی آن از حوصله این بحث خارج است.

در اشکال زیر تنها به عدد بدست آمده اشاره می شود.

شکل روبرو یکی از نمونه های مشهور فرکتال ها است. که به خم وان کخ شهرت دارد.

بعد بدست آمده برابر ۱٫۲۶۱۸۵۹ می باشد.

خم وان کخ با بعد ۱,۲

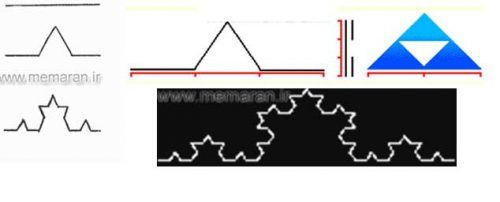
خم وان کخ با بعد ۱,۲

مجموعه ی کانتور با بعد .۰,۶۳۰۹۲۹  فرکتالی با بعد ۱,۵۸۴۹۶

فراکتال

منبع : pickcad.com